The Math Scam

by CalWatchdog Staff | June 26, 2012 8:26 am

June 26, 2012

[1]By Stan Brin

Some of us are good at math, some of us struggle merely to get through it.

Whether we’re good at it or bad, few of us will ever again use anything we learned in calculus or trigonometry class ever again, not even once. After graduation, few will even be able to recognize such general terms as sine and cosine, much less be able to explain what they mean.

For those who want to become engineers, scientists or economists, math is the foundation of their careers. It’s vital, not to be questioned.

For the rest of us — and I include technicians and medical workers* among the rest of us — math is, more often than not, a painful and soul-breaking ritual that we are forced to endure if we hope to have a decent life.

The official line is that lots and lots of math is supposed to prepare us for work. It’s supposed to teach us to think logically. It’s also supposed to help America compete against Asian Tiger economies that are eating our national lunch.

These assumptions may be mistaken. For many, if not most students, math education, at least as taught in this country, is little more than a cruel and expensive obstacle course designed to force large numbers of them to fail.

Even wore, this torture machine produces generations of Americans who graduate utterly unprepared to tackle real-world studies.

Consider the following sample problem that all students bound for higher education are expected to understand:

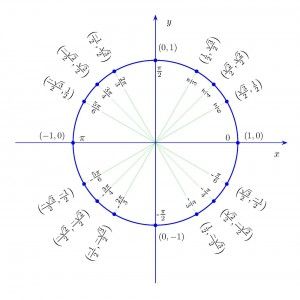[2]Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle.

This requirement, taken word for word from page 60 of the California Common Core standards, is among the norms used by 45 states and the District of Columbia to determine what every student should know. There are many, many, more examples, all equally opaque.

Obviously, somebody in 45 states and D.C. really thinks that all of us common folk really, really, need to know how to “traverse counterclockwise around the unit circle” or we won’t be able to think logically, as if mathematicians are known for their logical thinking. (Ted Kaczynski, Paul Erdos, Lord Bertrand Russell, John Nash, and Sir Isaac Newton come to mind — all of them brilliant, all of them mentally handicapped in various ways.)

During my career, I’ve written thousands of articles on subjects as varied as boxing and physics, I’ve designed software products that won two Editor’s Choice awards, but I’ve never had occasion to “traverse counterclockwise around the unit circle,” nor even to traverse it clockwise. Not once.

Nor did I ever have to understand “how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers.” In fact, I don’t even know what a unit circle or a coordinate plane is, or why anyone would want to traverse one. I’ve looked it up, and I still don’t know, other than the unit circle has something to do with a radius of a circle being equal to “one.” One what, no one says, at least not in English.

Of course, I’m sure that some people actually need to know all about the unit circle. I would include among them such truly and honest-to-gosh smart people as scientists, engineers, economists and artillery officers.

My brother, for example, needs to understand the unit circle. So does his wife. They’re both astrophysicists. They study the paths of comets and asteroids, and how to send space probes to meet them, what is known colloquially as “rocket science.”

Brainy folk like my brother — his face is familiar to the millions who like “history of the planets” shows — may account for 1 percent of the entire population. To that 1 percent, let’s add people whose work requires them to talk to scientists, engineers, economists and artillery officers, and we may have another 1 percent of the population. Let’s add another two percent for people who marry scientists, engineers, economists and artillery officers and those who know how to talk to them. Let’s also add another percentage point for math hobbyists who are actually interested in traversing the unit circle for its own sake – and we have a total of 5 percent, one out of 20.

And that’s being extremely generous.

The rest of us, 19 out of 20, are force fed higher math for up to four years. All college-bound students are required to pass three years of it. Vast numbers drop out in frustration, others manage to barely get by– and swear that they will never enter a classroom again.

And a day after our last finals, all of us who passed immediately forget absolutely everything. Meanwhile, very, very, few of us are taught how to use math to solve real-world problems, such as how to calculate the amount of wood needed to build a house, or how much concrete is required to pave a patio.

The average homeowner doesn’t have much use for the unit circle, but knowing how to buy just the right amount of materials, how to have it delivered on time and how much it will cost down the line, would save a lot of time and money.

But that’s not as important.

Blame History

There are those who believe that degrees are pointless scraps of paper. I disagree, but Peter Thiel and others have a point: We force young people to suffer obscure and useless subjects as a ritual — because it’s the way things are done, and the way things have always been done.

These obstacle courses — and that’s what they are, obstacles disguised as courses — exist because our grandparents and great-grandparents endured them, and if they learned to traverse the unit circle, well, by jiminy, today’s young whippersnappers had better learn to do it as well. We may no longer be expected to learn Latin and Classical Greek, thank Almighty Zeus, but the struggle with theoretical math still holds a mystical, untouchable holiness among well-meaning educators.

And yet very few young people study computer programming in high school, and those who do, don’t learn enough to obtain an entry level position. Think about it, 35 years into the PC age, and most kids put on their blue caps and gowns without ever learning Boolean logic, conditional loops, variables and arrays, terms that should actually mean something to the average, reasonably educated person.

Why? Because the starched-collared, monocle-wearing worthies who invented secondary education curricula for the unwashed masses, back in the olden days of bustles, shirtwaists, handlebar mustaches and buggy whips, didn’t think that practical subjects were as important as the skills they mastered at their exclusive private schools — such as translating Ovid or Caesar’s Gallic Wars.

Nevertheless, by 1900 times had changed. According to Professor Mark Ellis of Cal State Fullerton, a specialist in the history of math education, “The turn of the 20th century was the first era of large cities with diverse populations. Child labor was banned. Kids had time to go to school.”

The result was a vast increase in demand for secondary education, but the idea that students born of farmers or immigrant shopkeepers should study bookkeeping instead of Pericles’ Funeral Oration was difficult for academics from privileged backgrounds to understand.

Still, courses such as “shop” and “home economics” managed to infiltrate the system. Boys used to learn how to saw lumber, and girls learned how to cook. Perhaps, these days, boys and girls should study both subjects, or at least learn how to operate a microwave. Instead, they’re cramming math, yet falling even further behind international standards.

Latin and Classical Greek are now out of fashion, praise Jove and all the others. A few might want to study these languages so that they can name new species of slugs and jellyfish. (These days, dinosaurs are mostly given Chinese names.)

But California law still requires three years of higher math, including calculus from anyone who wants to go to the University of California or Cal State to study marketing, public administration or even history.

This doesn’t mean that that there are any monocled, pointy-bearded men and pince-nez wearing women out there eager to paddle the daylights out of nineteen out of twenty students with wooden rulers for failing to traverse the unit circle. Far from it. Their modern incarnations, such as Gerardo Loera, executive director of curriculum and instruction of the Los Angeles Unified School District, mean well. They just don’t get it.

“It should be as embarrassing to say ‘I can’t do math’ as it is to say ‘I can’t read,’” Loera says, which would make sense in a perfect world. “I still believe that math skills, such as critical thinking and problem solving, will transfer to other areas and are important even for liberal arts. Even if students don’t take any more math.”

Yet Loera, a fine and decent man who proved remarkably open and generous with his time, couldn’t cite any facts or figures to back up that belief. I asked him if calculus and trigonometry are useful in, say, journalism.

He sighed, and admitted that “I can’t cite any research that higher math helps journalists.”

Precisely my point.

 The Asian Solution

One reason why Asian countries seem to be eating our lunch appears to be an understanding of a basic fact of the human brain: Only so much stuff can be forced inside.

So they teach math from staple-bound booklets less than a hundred pages long. Only the most important topics are covered, but students are given time to actually understand them. Contrast those books to the dangerously heavy bricks California students are forced to lug home every day, and skim through because there’s no time to really understand what’s in them.

Everyone involved in teaching mathematics admits that the situation is ridiculous and self-defeating. According to a famous paper by Prof. William H. Schmidt of Michigan State University, the math curriculum in the United States is “a mile wide and an inch deep.”

Everyone involved in math education that I’ve talked to, including Cathy Seeley, a past president of the National Council of Teachers of Mathematics, agree with Schmidt: High schools are trying to cram too much into kids’ heads.

Courses cover too many topics in too little time, the teachers have to move on before the kids have time to absorb anything, the lessons are so abstract that they mean absolutely nothing, and in the end, the students will forget absolutely everything.

Some people claim that the problem isn’t topics — Singapore students, we are told, study more math topics than American students and do better on standardized tests.

But Singapore is an island city state. It has a small, rigorously conformist and highly disciplined population that accepts a single-party dictatorship without complaint. Singapore also famously produces university graduates who haven’t the slightest idea where babies come from. Even worse, chewing gum is illegal there.

It is also one of the countries whose students are expected to brutally cram for admissions tests. Once admitted, Asian students find that university studies are less rigorous than they are in North America, hence the vast numbers that come here for post-secondary education.

There are those who still believe that narrowing math standards in high school — and adding flexibility to the system — will cause California and the rest of the country to go to hell in the proverbial hand-basket. These should remember that American high schoolers have been doing poorly, by international standards, for decades, yet our universities are still the envy of the world.

An American Solution

I would never say that higher math is only for nerds, or that it is unnecessary for those interested in fields that build on its foundations, nor would I ever say that students shouldn’t know what trigonometry is, and why Newton invented calculus.

But instead of frying their brains trying to traverse the unit circle counterclockwise, perhaps students should be given a year of natural history. Instead of trying to solve useless, abstract puzzles, they should try to plot the orbit of a Mars probe, or how much energy would be required to send an asteroid hurtling to Earth to wipe out the dinosaurs. Or how scientists were able to use math to analyze regular mutations in DNA, proving that we are all descended from a single woman who lived some 200,000 years ago.

Or how King George III used calculus and astronomy to test the first practical longitudinal chronometer. (Yes, King George was the villain of the American revolution, but ancestors of most Americans arrived on this continent in reasonable safety, and at a much lower cost, because that very odd King was able to prove that the longitudinal chronometer actually worked — and convince others that it did.)

Students would find these examples more interesting than anything in the Core Curriculum. They might not be able to traverse that unit circle counterclockwise when they were finished, but they would know a few more things that they might remember past prom night.

———————————-

* Note: Doctors and nurses don’t need higher math. Perhaps some doctor might like to throw a quarrelsome hypochondriac from a window and calculate the time it takes him to land — that would be higher math. But in the real world, they mainly need to know the metric system and be able to keep its infernal decimal points in the right place. They have too much to learn about the infinite frailties of human anatomy to be bothered with traversing the unit circle. Try asking your surgeon a trig question, and you might as well be speaking Latin or Classical Greek, but he or she is still required to learn higher math as a way of demonstrating an intelligence sufficient to remove an appendix.

Source URL: https://calwatchdog.com/2012/06/26/the-math-scam/

---